From Maxwell to Kirchhoff

This entire chapter is devoted to the path from a full electromagnetic field description of microwave circuits governed by the Maxwell equations to a description in terms of electrical circuits governed by the Kirchhoff rules. A electrical circuit description of a given setup encompasses a network representation consisting of an arbitrary amount of two terminal devices. In our work we deal with three different kinds of two-terminal devices: capacitors, inductors and Josephson junctions. Every two-terminal device is characterized by a unique relationship between the current flowing through the device $I$ and the voltage difference at its two outlets $V$ . These relationships together with the Kirchhoff rules form a complete set of equations of motion for the currents and voltage drops across all two-terminal devices in the electrical circuit. This modular architecture of the theory entails the great advantage of flexibility. Once all the relationships for the two terminal devices are known, which often affords a description of the two-terminal device in terms of electromagnetic fields, we can quickly combine these building blocks with arbitrary complexity without having to solve for the electromagnetic fields of the whole electrical circuit again. Kirchhoff rules however strictly only apply in static situations. 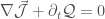They are consequences of the continuity equation of electrical charge: $\nabla \mathcal{\vec{J}}+\partial_t \mathcal{Q} = 0$ with current- $\mathcal{\vec{J}}$ and charge density $\mathcal{Q}$ . 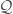If you consider the node of a electrical circuit, integrate the continuity equation in a sphere which is small enough to only include the node and neglect temporary accumulation of charge on the node, we come up with the first Kirchhoff rule: $\sum_{k\in \text{node}} I_k = 0$ , the sum of all currents flowing to the node of a electrical circuit is zero. This is valid as long as the characteristic timescale for changes in the current is not small enough to introduce charge accumulation on the node. We can circumvent however this difficulty by introducing an additional capacitor connected to ground for the node. For the second Kirchhoff rule it is more challenging to push the high frequency limit. 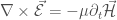For the second Kirchhoff rule we integrate $\nabla\times\mathcal{\vec{E}}=-\mu \partial_t \mathcal{\vec{H}}$ over a surface framed by a mesh of the electrical circuit. 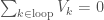If we again neglect the temporal accumulation of flux threaded through the mesh we come up with the second Kirchhoff rule: $\sum_{k\in \text{loop}} V_k = 0$ , the sum of all electrical voltage drops around every loop of the electrical circuit is zero. Lets suppose our circuit oscillates with frequency $\omega$ in a steady state. 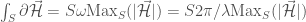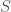Then the integral over the curl of the electric field can be approximated to $\int_S \partial \mathcal{\vec{H}}= S \omega \text{Max}_S(|\mathcal{\vec{H}}|)= S 2\pi /\lambda \text{Max}_S(|\mathcal{\vec{H}}|)$ , with $S$ the surface framed by the mesh and $\lambda$ the wavelength. In other words it is sufficient if the physical size of the electrical circuit is small compared to the wavelength of the excitations of the circuit for the description in terms of Kirchhoff rules to be valid.
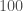
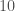
A typical low-frequency ( $\approx 30 \text{MHz}$ ) resonating circuit consists of a inductor coil and a parallel plate capacitor. If we reduce the size of the whole device by a factor of $100$ we would multiply the eigenfrequency by the same factor. The internal damping of the wiring of the resulting microwave resonating circuit would however also be $10$ times more effective. If we instead reduce the number of turns in the coil and increase the distance of the parallel plate capacitor we end up at a hairpin-shaped circuit, resonating in the microwave regime. The resulting electrical circuit however would be of the size of the wavelength of the microwaves itself. Two main differences compared to low-frequency circuits will arise from this. Firstly the circuit will start acting as an antenna and if we do not provide some means of shielding the circuit, there will be considerable radiative loss. Secondly the concept of inductors and capacitors as physical objects will fade and get replaced as a means to symbolically represent much more complicated structures where a physical object can be inductor and capacitor at the same time. To find the requirements for the existence of these symbolical representations is the purpose of this chapter.
Circuit QED setups typically consist of two different types of structures: coplanar transmission lines and lumped element structures. While the coplanar transmission lines are comparable to the wavelength, the lumped element structures like Josephson artificial atoms, coupling capacitors or Josephson junctions are considerably smaller than the wavelength. For the latter the low-frequency concepts do apply but the open transmission lines and transmission line resonators do need a special treatment. As it turns out the axial symmetry and the shielding by the groundplane are necessary ingredients to reintroduce the low-frequency concepts of capacitance per unit length of transmission line, or characteristic capacitance, and the inductance per unit length, or characteristic inductance.